생각하는 아이들

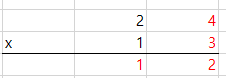
초등 3학년 - 수와 연산 : 분수와 소수,덧셈과 뺄셈,나눗셈 - 도형 : 평면도형, 원 - 길이와 시간,무게측정 - 자료의 정리 3학년 1학기 때에 분수라는 것을 배워 보았는데요. 2019/10/20 - [교과수학/3-1] - 3학년 1학기 똑같이 나누기 불러오는 중입니다... 한바구니에 담긴 구슬이 8개가 들어 있는데... 이것을 두 사람에게 똑같이 나누어 주려고 합니다. 이때 한사람에게 4개씩을 나누어 주게 되는데요. 이것을 전체를 1바구니를 2명으로 나눈 수 1/2 라고 표현합니다. 구슬 8 개를 2로 나눈 수 1/2은 4개가 되는데 이것은 4로 나눈수 2개 1/4 을 2개 합한 수와 동일하게 됩니다. 1/4 + 1/4 = 2/4 (4개) = 1/2(4개) 그렇다면 사탕 20개를 똑같이 5묶음으로..

초등 3학년 - 수와 연산 : 분수와 소수,덧셈과 뺄셈,나눗셈 - 도형 : 평면도형, 원 - 길이와 시간,무게측정 - 자료의 정리 원의 중심이란 컴퍼스로 원을 그릴때 중심이 되는 중심점을 의미합니다. 이때 원의 중심에서 원위의 한점과의 거리를 반지름이라고 합니다. 위와 같은 원이 있을때 A는 원의 중심, 선분 AC 또는 AB는 원의 반지름이라고 합니다. 또한 중심점을 지나는 원위의 두 점을 이은 선분 BC는 원의 지름이라고 합니다. 이때 원의 지름의 성질을 살펴 보면, 원의 지름은 한개의 원을 이등분하는 성질을 갖습니다. 또한 원의 지름은 원안에서 선분을 그을 수 있는 것중에 가장 깁니다. 원의 지름의 성질 중 하나는 원의 지름은 원의 반지름의 2배입니다. 그렇다면 위와 같은 원의 AC의 반지름이 2cm..

길동이는 순환소수가 왜 같은 수를 반복하게 될 수 밖에 없는지 그 이유가 무척 궁금했습니다. 길순이에게 혹시 그 이유가 무엇인지 물어 보았는데요. 길순이도 어떻게 설명을 해야 될지 모르다가... 멋적게 다음과 같이 설명을 이어 나갔습니다. 1/7 을 소수로 만드는 과정을 적어 볼래? 길동이는 다음과 같이 계산을 해 보았습니다. 길순이가 말했습니다. 나머지가 1 -> 3 -> 2 -> 6 -> 4 -> 5 -> 1 이 되고 다시 1이 반복 되므로 순환이 될 수 밖에 없는 거야. 여기서 7의 나머지가 0 이 되는 경우가 나타나면 순환이 끝나는 유한소수가 되는 것이지. 이때 1에서 다시 1이 되는 구간이 6마다 다시 돌아 오는 것을 순환마디라고 하거든... 그렇다면 1/13의 순환마디는 무엇일까? 정답) ....

길동이가 길순이에게 물었습니다. "길순아 어떤 경우가 유한소수가 되는지 알고 있어?" "그야 분모가 2와 5로만 소인수 분해 되는 분수가 유한소수지. 가령 10과 같은 경우 소인수 분해 하면 2와 5의 조합으로 구성되잖아" 여기서 잠깐 살펴 볼께요. 3/10 = 0.3, 7/20 = 0.35 (여기서 20은 2 x 2 x 5) ... "그래 맞아 그런데 분모가 7이거나 12 같은 경우는 소인수 분해 된 수에 2와 5가 아닌 수가 포함되어 있어서 순환소수가 되는 거지" 그런데 갑자기 길순이는 분모가 2와 5의 조합이 아닌 수일때는 순환소수가 되는 지 무척이나 궁금해 졌습니다. 그래서 길순이는 길동이에게 물었어요. "왜 2와 5의 조합이 아닌 조합에서는 순환소수가 되는거야?" 길동이 대답했어요. "그건 우리..

이런 방법으로 모두 낱장으로 만들려면 총 11번의 칼질이 필요합니다. 그렇다면 m x n 크기의 우표는 몇번만에 자를 수 있을까요? 정답) ...더보기 먼저 가로로 잘라서 m×1크기의 우표로 만들어 봅시다 이렇게 자르면 n-1 회로 m x 1크기의 우표가 n개 생깁니다. 잘라진 m×1크기의 우표를 1×1크기의 우표로 만들려면 자르기가 몇 번 필요할까요? m-1 회로 1 x 1 크기 우표로 만들 수가 있는데요. 그렇다면 n개를 이렇게 자르기 위해서는 n x (m-1) 회입니다. 이렇게 자른 횟수를 모두 더해 보면 n-1 + n x (m-1) 회가 됩니다.

초등 3학년 - 수와 연산 : 분수와 소수,덧셈과 뺄셈,나눗셈 - 도형 : 평면도형, 원 - 길이와 시간,무게측정 - 자료의 정리 3학년 1학기때 배운 내용 중에 빵 6개를 3명이서 똑같이 나누어 먹으면 2개씩 먹을 수 있다는 것을 확인했는데요. 만약에 빵 7개를 3명이서 똑같이 나누어 먹는다면 2개씩 먹으면 빵이 하나가 남는데요. 이것을 나머지라고 합니다. 즉 6 ÷ 3 = 2 --- 0 이라고 쓰며 6나누기 3의 몫은 2이고 나머지는 0 이라고 읽습니다. 7 ÷ 3 = 2 --- 1 이라고 쓰며 7 나누기 3의 몫은 2이고 나머지는 1이라고 읽습니다. 그렇다면 29 ÷ 3 의 몫과 나머지는 어떻게 될까요 몫은 9 가 되고 나머지는 2가 남습니다. 검산을 하는 방법은 몫 9 와 나누는 수 3 을 곱해 ..

초등 3학년 - 수와 연산 : 분수와 소수,덧셈과 뺄셈,나눗셈 - 도형 : 평면도형, 원 - 길이와 시간,무게측정 - 자료의 정리 3학년 1학기에 똑같이 나누기에서 나눗셈을 배워 보았는데요. 2019/10/15 - [/3-1] - 3학년 1학기 - 똑같이 나누기 불러오는 중입니다... 빵 6개를 3명이서 나누어 먹는 경우를 6 ÷ 3 이라고 표현하고 값은 2가 되었습니다. 오늘 배울 내용은 두자리수를 한자리수로 나누는 방법에 대해 알아 볼께요. 만약 지난번에 배운 빵의 갯수를 10배를 해 보겠습니다. 그렇다면 빵 60개를 3명이서 나누어 먹는 경우는 60 ÷ 3 으로 표현합니다. 이것을 계산하는 방법은 십단위 6을 3으로 먼저 나누어 봅니다. 여기서 몫이 2가 되는데 이 몫 2의 의미는 20의 의미가 됩..

초등 3학년 - 수와 연산 : 분수와 소수,덧셈과 뺄셈,나눗셈 - 도형 : 평면도형, 원 - 길이와 시간,무게측정 - 자료의 정리 3학년 1학기에는 두자리수 곱하기 한자리수를 계산하는 방법에 대해 알아 보았는데요. 3학년 2학기에는 두자리수 곱하기 두자리수를 계산하는 방법에 대해 알아 볼께요. 만약 24개 짜리 묶음이 13개 있다고 하면 24 x 13 으로 계산을 하면 됩니다. 그렇다면 3학년 1학기에 배운 2자리수 곱하기 한자리수를 생각해 보겠습니다. 먼저 24 X 3 을 먼저 계산하면 72 가 됩니다. 그러면 24 X 10 이 남는데요 이것을 계산하면 240 이 됩니다. 따라서 240 + 72 = 312 가 됩니다. 이렇게 계산하는 방법을 살펴 보면 다음과 같이 계산을 해 볼 수가 있겠네요. 먼저 빨..

초등 3학년 - 수와 연산 : 분수와 소수,덧셈과 뺄셈,나눗셈 - 도형 : 평면도형, 원 - 길이와 시간,무게측정 - 자료의 정리 드디어 3학년 2학기가 되었네요. 길동이는 개학을 하면서 학교 준비물이 성냥이라서 문구점에 가서 성냥통을 샀는데요. 성냥통 5개를 샀습니다. 그런데 길동이가 쉬는 시간에 이 성냥통 하나에 성냥개비가 몇개가 있는지 무척이나 궁금한거예요. 그래서 성냥통 하나를 뜯어서 성냥개비를 세었습니다. 그런데 성냥통 하나에는 성냥개비가 327개가 있네요. 그렇다면 길동이가 센 성냥개비는 모두 몇개일까 고민을 해 보니... 327 + 327 + 327 + 327 + 327 으로 계산을 했어요. 이렇게 보고 있던 길순이가... 3학년 1학기때 곱셈을 배웠는데 그걸 이용하면 되지 하면서 곱셈을 하..

초등 3학년 - 수와 연산 : 분수와 소수,덧셈과 뺄셈,나눗셈 - 도형 : 평면도형, 원 - 길이와 시간,무게측정 - 자료의 정리 지난시간에 소수에 대해 알아 보았습니다. 2019/10/23 - [/3-1] - 3학년 1학기 소수 알아보기 불러오는 중입니다... 오늘은 소수의 크기에 대해 살펴 보겠습니다. 1.5 를 그림으로 살펴 보면 다음과 같습니다. 2.1을 그림으로 살펴 보면 다음과 같습니다. 그림으로 보듯이 1.5는 0.1이 15개입니다. 2.1은 0.1이 21개입니다. 따라서 1.5 < 2.1 입니다. 이렇게 소수를 비교하는 방법 1.5 < 2.1 의 크기 비교는 먼저 자연수 부분 1 과 2 중에 자연수 부분이 큰 것이 소수가 더 큽니다. 만약 자연수 부분이 같은 3.4 와 3.7 과 같은 경우..