| 펜윅트리(Fenwick Tree)란? |
- Binary Indexed Tree 라고도 하며 이진수를 이용하여 위치값을 표현하는 세그먼트 트리와 유사한 트리
| 펜윅트리(Fenwick Tree) 의 개념 |
10진수 수를 이진수로 표현해 보면 다음과 같다.
3 = 00000011
4 = 00000100
5 = 00000101
6 = 00000110
8 = 00001000
9 = 00001001
10 = 00001010
11 = 00001011
12 = 00001100
16 = 00010000
여기서 이진수의 마지막 1의 위치를 확인하면 다음과 같다.
3= 왼쪽에서 첫번째 자리 (10진수의 값으로 1)
4= 왼쪽에서 3번째 자리 (10진수의 값으로 4)
5= 왼쪽에서 첫번째 자리(10진수의 값으로 1)
...
16 = 왼쪽에서 5번째 자리(10진수의 값으로 16)
이러한 값을 저장하는 L[i]라고 표현 한다고 하면
L[3]=1,L[4]=4,L[5]=1,....,L[16]=16 이라고 표현할 수 있다.
수 N개를 A[1]~A[N] 이라고 했을 때 Tree[i]는 A[i] 부터 앞 방향으로 L[i]개의 합을 저장한다.
그림으로 살펴 보면 다음과 같다.
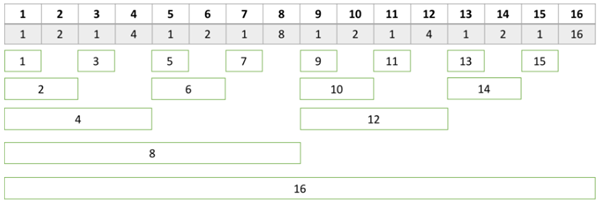
여기서
Tree[1] 에는 A[1]~A[1] 까지의 합
Tree[2] 에는 A[1]~A[2] 까지의 합
Tree[3] 에는 A[3]~A[3] 까지의 합
...
Tree[8] 에는 A[1]~A[8] 까지의 합
과 같은 형태로 저장이 된다.
| 합의 갯수 L[i] 를 구하는 방법 |
L[i] = i & -i
※ -i 의 값은 ~i + 1 과 같다.(음수는 2의 보수의 값을 취한다. 2의 보수는 1의 보수 + 1)
예)
i = 100110101110101100000000000
~i = 011001010001010011111111111
-i = 011001010001010100000000000
i & -i = 000000000000000100000000000
따라서 왼쪽에서 첫번째 나오는 자리의 위치 값을 구할 수 가 있게 된다.
| Tree[i] 에 값을 저장하는 방법 |
A = [3, 2, 5, 7, 10, 3, 2, 7, 8, 2, 1, 9, 5, 10, 7, 4]

Tree[8] 에는 A[1]~A[8] 까지의 합 39가 저장된다.
| Tree 배열을 이용해서 처음 부터 합 구하기 |
A[1]+A[2]+...+A[13] 의 값을 구해 보자.

위의 표에서 확인을 해 보면 Tree[8] + Tree[12] + Tree[13] 인 것을 확인 할 수 있다.
13을 이진수로 나타내면 1101 이다.
여기서 Tree[1101] + Tree[1100] + Tree[1000] 인것을 알 수 있다.
즉 마지막 1의 위치를 없애면서 해당 위치의 Tree 값을 누적해 가는 원리이다.
마지막 위치의 1을 없애는 방법
i = i - (i & -i) /// 현재 i 의 위치에서 마지막 1의 위치의 값을 빼면 마지막 위치의 1이 없어진다.
| Tree 배열을 이용해서 처음 부터 합 구하기 구현 |
|
1
2
3
4
5
6
7
8
9
|
int sum(int i) {
int ans = 0;
while (i > 0) {
ans += tree[i];
i -= (i & -i); //이진수에서 마지막 위치의 1을 뺀다.
}
return ans;
}
|
cs |
| Tree 배열에 입력된 데이터 갱신하기 |

그림에서 A[5]이 갱신되면 Tree[5],Tree[6],Tree[8],Tree[16] 의 값을 갱신해 주어야 한다.
이진수로 표현하면 5은 0101 이고
6번지는 0110
8번지는 1000
16번지는 10000
번지수를 확인해 보면 마지막 위치의 1의 자리에 1을 더해 주면 되는 원리이다.
0101 + 0001 = 0110
0110 + 0010 = 1000
1000 + 1000 = 10000
위와 같은 원리로 찾아가는 번지는 i = i + (i & -i) 와 같다.
| Tree 배열에 입력된 데이터 갱신하기 구현 |
|
1
2
3
4
5
6
7
|
void update(int i, int num) {
while (i <= n) {
tree[i] += num;
i += (i & -i); //이진수에서 마지막 위치의 1을
}
}
|
cs |
| Tree 배열을 이용해서 구간합 구하기 |
A[7]~A[13] 까지의 합을 구하는 방법은
sum(13) - sum(6) 와 같이 구하면 됨
| 펜윅트리를 이용한 최대값(또는 최소값) 구하기 |
구간합은 비교적 간단하게 구할 수 있지만 펜윅트리를 활용한 최대값(또는 최소값) 은 약간 다르다.
가령 A[3]~A[9] 의 최소값을 찾는다고 하면 A[1]~A[9] 의 최소값을 찾은 후 A[1]~A[2] 의 최소값을 뺄수가 없는 형태이기 때문이다.
따라서 이런 경우 두개의 펜윅트리를 사용하게 되는데 원리는 다음과 같다.

첫번째 트리는 앞에서 부터의 최소값을 저장한다.
두번째 트리는 뒤에서 부터의 최소값을 저장한다.
이 경우 두번째 트리에서 3과 9 사이의 최소값 2 와 첫번째 트리 9부터 3까지의 최소값 중 최소값을 선택하면 된다.
선택하는 방법은 다음과 같다.
1. 두번째 트리에서 BTree[3] 위치의 5를 선택
2. 두번째 트리에서 BTree[4] 위치의 2를 선택
3. 두번째 트리에서 BTree[8] 위치를 선택할 차례인데 BTree[8] 의 범위는 A[8]~A[15] 까지의 영역이므로 종료
(단, 여기서 A[8] 위치의 값 7 을 선택)
4. 첫번째 트리에서 ATree[9] 위치의 8을 선택
5. 첫번째 트리에서 ATree[8] 위치를 선택할 차례인데 ATree[8] 의 범위는 A[1]~A[8] 까지의 영역이므로 종료
| 소스코드 예제 |
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
void update(int i,int num)
{
while (i<=N)
{
tree[i]=min(tree[i],num);
i += (i& -i);
}
}
void update2(int i,int num)
{
while (i>0)
{
tree2[i]=min(tree2[i],num);
i -= (i& -i);
}
}
int query(int a,int b)
{
int v = MAX;
int prev = a;
int curr = prev + (prev & -prev);
while(curr <= b)
{
v=min(v,tree2[prev]);
prev=curr;
curr=prev + (prev & -prev);
}
v = min(v,arr[prev]);
prev = b;
curr = prev - (prev & -prev);
while(curr >= a)
{
v = min(v,tree[prev]);
prev=curr;
curr=prev -(prev & -prev);
}
return v;
}
|
cs |
'정보 > 알고리즘' 카테고리의 다른 글
| [알고리즘] LIS(Longest Increasing Subsequence - 최장증가부분수열) (0) | 2021.03.18 |
|---|---|
| [알고리즘] Dynamic(동적프로그래밍) (0) | 2021.03.18 |
| [알고리즘] Segment Tree(세그먼트 트리) (0) | 2021.03.18 |
| [알고리즘] Heap(힙) 정렬[알고리즘] Heap(힙) 정렬 (0) | 2021.03.18 |
| [알고리즘] Breadth First Search (너비 우선 탐색) (0) | 2021.03.15 |