초등 4학년
- 수와 연산 : 큰수,곱셈과 나눗셈,분수의 덧셈과 뺄셈,소수의 덧셈과 뺄셈
- 규칙찾기
- 도형 : 평면도형의 이동, 삼각형, 사각형, 다각형
- 측정 : 각도
- 막대그래프,꺽은선 그래프
각의 크기는 변의 길이와 상관없이 두 변의 벌어진 정도가 클 수록 큰 각입니다.

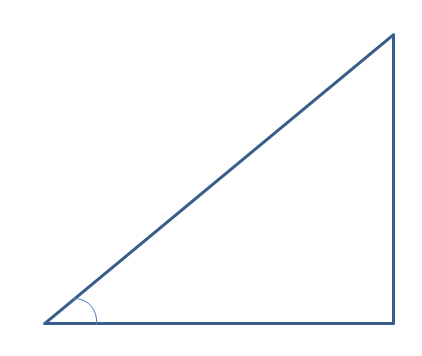
위의 그림에서 두변의 벌어진 정도가 큰 것은 오른쪽 보다 왼쪽이 더 큽니다.
각의 크기를 각도라고 하며,
직각을 90도 라고 하며 90도를 90등분 한 것 중 하나를 1도라고 합니다.
또한 직각 보다 작은 각(0도 보다 크고 90도 보다 작은 각) 을 예각 이라고 합니다.
직각 보다 크고 180도 작은 각을 둔각 이라고 합니다.
각도의 계산
각도의 합과 차는 자연수의 덧셈 뺄셈과 같은 방법으로 계산 합니다.
즉
20도 + 60도 = 80도
60도 - 20도 = 40도
와 같이 계산합니다.
삼각형의 세 각의 크기
삼각형의 종이를 잘라서 세꼭짓점이 한 점에 모이도록 이어 붙이면 180도가 됩니다.
이렇게 여러개의 모양과 크기의 삼각형을 잘라서 세 꼭짓점이 한점에 모이도록 이어 붙이면 180도가 되는 것을 확인 할 수 있습니다.
따라서 모양과 크기에 상관없이 모든 삼각형의 세 각의 크기의 합은 180도가 됩니다.
사각형의 네 각의 크기
사각형의 종이를 네 조각으로 잘라서 네 꼭짓점이 한점에 모이도록 이어 붙이면 360도가 됩니다.
여러가지 모양의 사각형 여러 크기의 사각형을 잘라서 네 꼭짓점이 한점에 모이도록 이어 붙이면 360도가 되는 것을 확인 할 수 있습니다.
따라서 모양과 크기에 상관없이 모든 사각형의 네 각의 크기의 합은 360도가 됩니다.
오각형의 다섯 각의 크기
오각형의 종이를 다섯 조각으로 잘라서 다섯 꼭짓점이 한점에 모이도록 이어 붙이면 540도가 됩니다.
여러가지 모양의 오각형 여러 크기의 오각형을 잘라서 다섯 꼭짓점이 한점에 모이도록 이어 붙이면 540도가 되는 것을 확인 할 수 있습니다.
따라서 모양과 크기에 상관없이 모든 오각혁의 다섯 각의 크기의 합은 540도가 됩니다.
위와 같이 다각형의 꼭짓점의 합을 살펴 보면 다음과 같습니다.
삼각형 - 180
사각형 - 360
오각형 - 540
이렇게 다각형의 각이 한개씩 늘어 날때마다 내각의 합은 180도씩 늘어 나는 것을 확인 할 수 있습니다.
그렇다면 육각형의 꼭짓점의 합을 모두 합하면 얼마일까요?
정답)
육각형의 내각의 합은
오각형 내각의 합 540도 보다 180도가 더 큰 720도 입니다.
'교과수학 > 4-1' 카테고리의 다른 글
| 4학년 1학기 세자리수 나누기 두자리수 (0) | 2019.12.29 |
|---|---|
| 4학년1학기 - 세자리수 곱하기 몇십 (0) | 2019.12.28 |
| 4학년 1학기 - 수의 크기 비교 (0) | 2019.12.02 |
| 4학년 1학기-큰수 알아보기(억,조) (0) | 2019.12.01 |
| 4학년 1학기 - 큰 수 알아 보기 (0) | 2019.11.29 |