2차원 펜윅트리에 앞서 1차원 펜윅트리에 대해 알아보자.
https://thinkmath2020.tistory.com/709
[알고리즘] Fenwick Tree(펜윅트리) :: 생각하는 아이들
thinkmath2020.tistory.com
1차원 펜윅트리에 대해 이해를 했다면 이러한 1차원 배열을 여러개 이어 붙인 것을 2차원 펜윅트리라고 생각할 수 있다.
2차원의 구간합을 구하기 위해서 2개의 인덱스(y,x)가 필요하다.
그림으로 이해하면 다음과 같다.
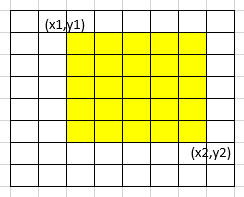
(x1,y1) ~ (x2,y2) 의 구간합을 구하는 방법을 살펴 보면
먼저 (0,0)~(x2,y2) 의 구간합을 구한다.

이때 녹색과 하늘색 부분인 (0,0) ~ (x1,y2), (0,0)~(x2,y1) 구역을 빼 주면 되는 것을 확인 할 수 있다.
이렇게 두개의 구간 합을 빼 주면 (0,0) ~ (x1,y1) 구간의 합이 두번 빠지는 것을 확인할 수 있다.
따라서 sum(x1,y1,x2,y2) = sum(0,0,x2,y2) - sum(0,0,x1,y2) - sum(0,0,x2,y1) + sum(0,0,x1,y1) 이 되는 것을 확인 할 수 있다.
이것을 펜윅트리로 구현하면 다음과 같이 구현 할 수 있다.
(y,x) 위치에 현재값과의 차이를 더하는 경우 (y,x) ~ (n,n) 까지 모두 업데이트 해 주면 된다.
이때 y~n 까지 진행 역시 1차원 펜윅트리를 사용하여 이동하면 되고 x~n 까지 진행 역시 1차원 펜윅트리를 사용하면 되므로 코드는 다음과 같이 구현이 가능하다.
void update(int y, int x, int diff){
for(int i = y; i <= N; i += (i & -i)) ///행을 이동하면서
for(int j = x; j <= N; j += (j & -j)) /// 해당 열의 뒷쪽을 모두 그 차이만큼 더하자
BIT[i][j] += diff;
}(0,0) ~ (y,x) 까지의 구간합을 구하는 함수를 살펴 보면 1차원 펜윅트리를 이용하여 다음과 같이 구할 수 있다.
long long sum(int y, int x){
long long res = 0;
for(int i = y; i > 0; i -= (i & -i))
for(int j = x; j > 0; j -= (j & -j))
res += BIT[i][j];
return res;
}(y1,x1) ~ (y2,x2) 범위의 합을 구해 오는 함수를 살펴 보면 다음과 같이 구현이 가능하다.
long long query(int y1, int x1, int y2, int x2){
return sum(y2, x2) - sum(y2, x1 - 1) - sum(y1 - 1, x2) + sum(y1 - 1, x1 - 1);
}
'정보 > 알고리즘' 카테고리의 다른 글
| 문자열알고리즘-트라이(TRIE) (0) | 2022.01.02 |
|---|---|
| SPFA(Shortest Path Faster Algorithm) (0) | 2021.10.23 |
| 인터랙티브 1 (0) | 2021.06.30 |
| DP최적화 (0) | 2021.06.30 |
| 기하2 (0) | 2021.06.30 |