1. 케라스
케라스는 신경망 모델을 구축할 수 있는 고수준 API 라이브러리이다.
1.1 인공신경망
인공신경망(Aritficial Neural Network - ANN)은 두뇌의 신경세포인 뉴런을 수학적으로 모방한 모델이다.
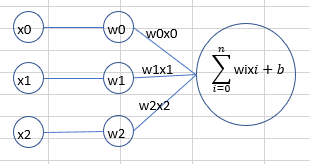
인공신경망을 수학적으로 표현하면 위의 그림과 같이 된다.
그림에서 3개의 입력갑을 받아 1개의 출력값을 내 보내는데 뉴런에 들어온 입력값이 임계치를 넘어 활성화 되면 출력값을 내보내게 된다.
즉 인공신경망에서 뉴런이라는 함수의 입력값에 x0,x1,x2를 집어 넣었을때 임의의 가중치(w0,w1,w2) 및 편향값(b)의 값에 의해 출력값 0 또는 1 이 나온다고 생각하면 된다.
이 때 가중치와 편향값은 뉴런의 동작 특성을 나타내는 중요한 파라미터로 이 값들을 조정해서 원하는 출력값을 만들어 내는 것이다.
위의 결과값은 다음과 같은 수식에 의해 결정된다.
y= (w0x0 + w1x1 + w2x2) + b
실제 뉴런은 입력된 신호가 특정 강도 이상일 때만 다음 뉴런으로 신호를 전달한다. 이와 마찬가지로 인공신경망에서도 동일한 역할을 하는 영역이 있는데 이것을 활성화 함수라고 한다.
활성화함수는 여러종류가 있는데 여기서는 3가지 활성화 함수에 대해 알아 보자.
1) 스텝함수(step function) : 그래프 모양이 계단과 같아 스텝함수라고 하는데 입력값이 0 보다 클때 1, 0 이하는 0 으로 출력하는데 이 함수는 결과가 합격/불합격 과 같이 이진분류 문제일 때 사용한다.
하지만 스텝함수는 너무 극단적으로 나누기 때문에 문제가 있다. 예를 들면 0.0001 과 같은 경우 0 에 가깝지만 1로 출력 된다.
이런 문제를 확률을 이용해서 결과를 소수점으로 표현하는 것이 훨씬 자연스러운데 이진분류에서 이런 문제를 해결하기 위해 사용하는 활성화 함수는 시그모이드함수(sigmoid function)이다.
2) 시그모이드함수(sigmoid function)
시그모이드 함수는 다음과 같이 표현된다.
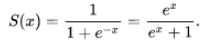
이 그래프는 S자형곡선 또는 시그모이드 곡선을 갖게 되는데 그래프는 다음과 같다.

시그모이드 함수는 신경망 초기에는 많이 사용되었지만 기울기소실 문제, 함수의 중심값이 0이 아닌 문제, exp함수 사용시 비용이 큰 문제와 같은 단점들 때문에 최근에는 ReLU 함수를 많이 사용하게 된다.
3) ReLU(Rectified Linear Unit)
ReLU 함수는 +신호는 그 값을, - 신호는 차단함수라고 하는데 그 생김새는 다음과 같다.

수식에서 보이듯이 양수이면 자신을 반환하고 음수이면 0 을 반환한다.
그래프는 다음과 같다.

실제로 문제를 신경망 모델로 해결 할 때는 1개의 뉴런만 사용하지 않고 복잡할 수록 뉴런의 수가 늘어 나야 하고 신경망의 계층도 깊어져야 한다.
입력층과 출력층으로만 구성 되어 있는 것을 단층신경망이라고 하며 1개 이상의 은닉층을 가지고 있는 신경망을 심층신경망(Deep Neural Network,DNN) 이라고 한다. 앞으로 나오는 신경망은 심층신경망이라고 생각하면 된다.

위와 같이 입력층과 은닉층을 거쳐 출력층까지 데이터가 순방향으로 전파하는 과정을 순전파(forward propagation) 라고 한다.
데이터가 순방향으로 전파될 때 현 단계 뉴런의 가중치와 전단계 뉴런의 출력값의 곱을 입력값으로 받고 다시 활성화 함수를 통해 다음 뉴런으로 전파 된다.
이때 출력값은 실제값과 오차가 발생하게 된다.

실제값은 7 인데 출력값은 1이 나왔다면 6의 오차가 발생한다.
성능 좋은 모델은 순전파의 결괏값이 실젯값의 차이가 크지 않은 모델을 의미한다. 즉 오차가 작은 모델일 수록 예측 정확도가 높다.
그럼 오차가 발생 했을 때 각 뉴런의 가중치를 어떻게 조정할까?

가중치 조정은 순전파의 역방향으로 진행 된다. 이때 각 단계별로 만나는 뉴런의 가중치가 얼마만큼 조정되어야 오차를 줄일 수 있는지 계산해 가중치를 갱신한다.
위의 그림에서는 오류가 6이라고 했지만 실제로는 (출력값 - 실젯값)^2 의 수식으로 표현 하는데 이것을 손실 함수라고 한다.
그림에서 w5의 변화량에 따른 (출력값-실젯값)^2 의 변화량을 구할 수 있는데 이 것을 다른말로 표현하면 (출력값-실젯값)^2 을 w5로 미분하는 것이다.
따라서 새로운 w5는 다음 수식으로 결정이 된다.
w5 - η * ( (출력값-실젯값)^2 ) 을 w5로 미분한 값
이런 일련의 과정을 역전파(back propagation)이라고 부르며 이러한 역전파를 이용해 오차를 최대한 줄일 수 있도록 가중치를 조정하는 과정을 의미한다.
1.2 딥러닝 분류 모델 만들기
케라스에서 제공하는 API 를 이용해 MNIST 분류 모델을 만들어 보자.
#필요한 모듈 임포트
import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np
from tensorflow.keras.datasets import mnist
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Flatten,Dense
#MNIST 데이터셋 가져오기
(x_train,y_train),(x_test,y_test) = mnist.load_data()
x_train,x_test = x_train/255.0, x_test/255.0 #데이터 정규화 이미지는 0~255 사이의 픽셀값으로 저장 되어 있는데 이것을 0~1 사이로 변환
print(x_train.shape,x_test.shape)
훈련데이터는 28*28 이미지 60000장 테스트 데이터는 28*28 이미지 10000 장인 것을 알 수 있다.
첫번째 이미지를 살펴 보자
plt.imshow(x_train[0], cmap='gray')
#tf.data를 사용하여 데이터셋을 섞고 배치 만들기
ds=tf.data.Dataset.from_tensor_slices((x_train,y_train)).shuffle(60000)
train_size = int(len(x_train)*0.7) #훈련데이터중 70프로는 훈련,30프로는 검증셋
train_ds = ds.take(train_size).batch(20) #배치사이즈를 20으로 설정
val_ds=ds.skip(train_size).batch(20)tf.data.Dataset.from_tensor_slices 는 x_train과 y_train 를 슬라이싱 하여 텐서 형태로 만들어 주는 함수(https://www.tensorflow.org/api_docs/python/tf/data/Dataset#from_tensor_slices 참고) 이며 shuffle(버퍼사이즈) 에서 버퍼사이즈는 데이터 크기보다 크거나 같게 설정해야 된다.
여기서 배치 사이즈는 학습 시 샘플 수를 의미하며 배치 사이즈가 작을 수록 가중치 갱신이 자주 일어 난다.
#MNIST 분류 모델 구성
model = Sequential()
model.add(Flatten(input_shape=(28,28))) #28*28 형태의 2차원 배열을 784 형태의 1차원 배열로 Flatten
model.add(Dense(20,activation='relu'))
model.add(Dense(20,activation='relu'))
model.add(Dense(10,activation='softmax'))케라스 모델을 만드는 방법은 순차 모델과 함수형 모델이 있는데 여기서는 순차모델(Sequential) 을 사용했다.
위에서 28*28 크기의 2차원 이미지를 1차원으로 평탄화(Flatten) 시킨 후
2개의 은닉층 Dense() 를 사용해 출력크기가 20이고 활성화 함수는 ReLU를 사용하도록 만들었다.
마지막으로 softmax를 사용하는 출력층을 만들었다. 0~9 까지의 숫자이므로 출력층의 크기를 10으로 지정했다.
여기서 Softmax 함수는 다음과 같은 역할을 수행한다.
입력받은 값을 출력으로 0~1 사이의 값으로 정규화 한다. 이 함수는 출력 값들의 총합이 항상 1이 되는 특징을 갖고 있어 결과를 확률로 표현할 수 있다. 따라서 분류하고 싶은 클래스 개수만큼 출력으로 구성하며 가장 큰 출력값을 가지는 클래스가 결괏값으로 사용된다.
#모델생성
model.compile(loss='sparse_categorical_crossentropy',optimizer='sgd',metrics=['accuracy'])위에서 정의한 신경망 모델을 실제로 생성하는 부분으로 손실함수는 sparse_categorical_crossentropy 를 사용했고 오차를 보정하는 옵티마이저로는 SGD 를 사용했다. 모델의 성능을 평가하는 측정항목으로는 accuracy를 사용한다.
여기서 손실함수 sparse_categorical_crossentropy는 모델의 결괏값과 실제 정답과의 오차를 계산하는 함수를 의미하는데 다중 클래스를 분류하는 문제에서는 sparse_categorical_crossentropy 를 사용하면 좋은 성능을 낼 수 있는 도구 정도로 생각하면 된다.
sparse_categorical_crossentropy 과 categorical_crossentropy의 차이 https://crazyj.tistory.com/153 참고
#모델 학습
hist = model.fit(train_ds,validation_data=val_ds,epochs=10)생성한 모델을 실제 학습한다. epochs의 값 만큼 학습을 수행하는데 epochs가 너무 커지면 과적합이 일어날 수 있으므로 적당한 값을 사용해야 한다.
#모델평가
print("모델평가")
model.evaluate(x_test,y_test)
evaluate 를 이용하여 성능을 평가하는데 인자에는 테스트용 데이터셋을 사용한다.
위의 결과는 정답율 94프로 정도인 것을 알 수 있다.
이렇게 만들어진 모델을 저장한다.
#모델저장
model.save('mnist_model.h5')
이렇게 모델을 저장해 놓으면 훈련된 모델만 사용하면 되므로 학습 없이 빠르게 사용할 수 있다.
#모델 확인
model.summary()만들어진 모델을 확인해 보면 다음과 같다.

이렇게 만들어진 모델을 불러와서 사용하는 방법은 다음과 같다.
from tensorflow import keras
reconstructed_model = keras.models.load_model("mnist_model.h5")
print("모델평가")
reconstructed_model.evaluate(x_test,y_test)
#학습결과 그래프 그리기
fig,loss_ax = plt.subplots()
acc_ax = loss_ax.twinx()
loss_ax.plot(hist.history['loss'],'y',label='train loss')
loss_ax.plot(hist.history['val_loss'],'r',label='val_loss')
acc_ax.plot(hist.history['accuracy'],'b',label='train acc')
acc_ax.plot(hist.history['val_accuracy'],'g',label='val_acc')
loss_ax.set_xlabel('epoch')
loss_ax.set_ylabel('loss')
acc_ax.set_ylabel('accuracy')
loss_ax.legend(loc='upper left')
acc_ax.legend(loc='lower left')
plt.show()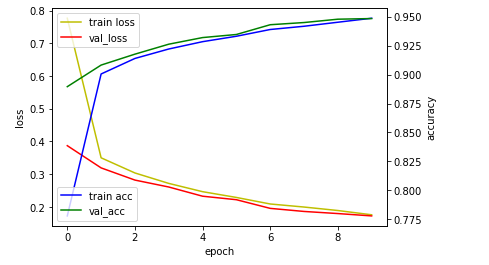
위의 그래프는 손실값(loss)와 정확도(accuracy)를 보여 준다.
x축은 에포크(학습횟수)를 의미하며 y축은 손실도와 정확도를 의미한다.
여기서 에포크값을 너무 크게 부여하면 오버피팅이 발행 할 수 있으니 주의해야 한다.
모델 학습시 정확도와 손실값이 어떻게 변화하는지 지속적으로 모니터링 해서 하이퍼 파라미터를 튜닝하는 작업을 좋은 결과가 나올 때까지 반복해야 한다.
1.3 학습된 딥러닝 모델 사용하기
바로 전에서 살펴 보았는데 어떻게 불러 오고 사용 방법을 실습을 통해 알아 보자.
모델을 사용할 때마다 매번 학습한다고 하면 사용할 때마다 학습 시간이 많이 걸리기 때문에 파일형태로 저장을 해 놓은 후 그 모델을 이용해서 데이터를 예측하게 된다.
from tensorflow.keras.datasets import mnist
from tensorflow.keras.models import load_model
import matplotlib.pyplot as plt
#MINIST 데이터셋 가져오기
_,(x_test,y_test)=mnist.load_data()
x_test=x_test/255.0 #정규화
#모델 불러오기
test_model = load_model('mnist_model.h5')
test_model.summary()
test_model.evaluate(x_test,y_test,verbose=2)
#테스트셋에서 20번째 이미지 출력
plt.imshow(x_test[20],cmap='gray')
plt.show()
#테스트셋에서 20번째 이미지 클래스 분류
piks=[20]
#predict = test_model.predict_classes(x_test[piks])
y_prob = model.predict(x_test[piks], verbose=0)
predict = y_prob.argmax(axis=-1)
print("손글씨 이미지 예측값",predict)predict_classes 사용시 오류가 발생하는데 2.6 버젼 이후로 predict_classes 가 지원되지 않는다.

결과값은 위와 같이 9를 예측한다.
참고]
한빛미디어- 처음 배우는 딥러닝 챗봇
'머신러닝 > 12. 딥러닝챗봇' 카테고리의 다른 글
| [딥러닝 챗봇] 챗봇 엔진에 필요한 딥러닝 모델 - LSTM (0) | 2022.06.24 |
|---|---|
| [딥러닝 챗봇] 챗봇 엔진에 필요한 딥러닝 모델 - CNN (0) | 2022.06.21 |
| [딥러닝 챗봇] 텍스트 유사도 (0) | 2022.06.20 |
| [딥러닝챗봇]임베딩 (0) | 2022.06.17 |
| [딥러닝챗봇]토크나이징 (0) | 2022.06.16 |