접미사 배열(https://thinkmath2020.tistory.com/3558) 자체만으로 해결 할 수 있는 문제는 거의 없다.
접미사 배열과 함께 중요한 개념인 LCP(Longest Common Prefix)를 살펴 보자.
LCP는 가장 긴 공통 접두사로 일반적으로 그 길이에 의미가 있다.
대부분의 상황에서 Suffix Array 에 쓰이는 개념이라고 볼 수 있다.
lcp[i]는 접미사 배열의 i번째 접미사와 i-1번째 접미사의 가장 긴 공통 접두사의 길이라고 정의 된다.
| 접미사 | num | lcp |
| a | 5 | x |
| ana | 3 | 1 |
| anana | 1 | 3 |
| banana | 0 | 0 |
| na | 4 | 0 |
| nana | 2 | 2 |
앞의 길이가 얼마만큼 크기가 같은지 찾아 주면 된다.
이때 앞에서 부터 하나씩 찾는다면 길이 n 에 대해 O(n^2) 의 시간 복잡도이지만 다음과 같이 처리하면 O(n) 의 처리 속도로 연산이 가능하다.
suffix 배열 SA[]= {5,3,1,0,4,2} 이라면
invSuff배열을 다음과 같이 해당 위치의 순서를 기록해 두자.(즉 역함수의 관계)
invSuff[] = {3,2,5,1,4,0}
즉 banana 는 3번지, anana 는 2번지,nana는 5번지,ana는 1번지,na는 4번지, a는 0번지에 있다는 의미이다.
Kasai’s Algorithm 을 이용해 푸는 방법은 다음과 같다.
1) 0번 위치의 banana 에서 다음 접미사는 na 이다.
suffix 에서 다음 접미사를 찾으려면 invSuff 배열 이용
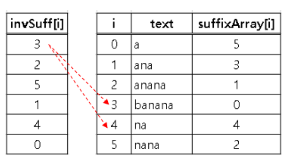
banana 와 na간 공통 접두사가 없으므로 LCP[3]=0
2) 1번 위치의 anana 에서 다음 접미사는 banana 이다.
공통 접두사가 없으므로 LCP[2]=0
3) 2번 위치의 nana 에서 다음 접미사는 없으므로 LCP 값은 정의 되지 않는다. 임의로 LCP[5]= 0 으로 할당.
4) 3번 위치의 ana 에서 다음 접미사는 anana 이므로 공통 접두사 길이 = 3 이므로 LCP[1] = 3
5) 4번 위치의 na 에서 다음 접미사는 nana 이므로 공통 접두사 길이 = 2 이므로 LCP[4]=2
6) 5번 위치의 a에서 다음 접미사는 ana 이므로 공통 접두사의 길이 = 1 이므로 LCP[0]= 1
LCP={1,3,0,0,2,0} 의 값을 찾을 수 있다.
참고 : https://zoosso.tistory.com/698
LCP (Longest Common Prefix)
LCP (Longest Common Prefix) LCP는 두 접미사의 최대 공통 접두사의 길이를 의미 ※ 앞서 접미사 배열(Suffix Array)에 대해서 알고 있어야 합니다. 접미사 배열(Suffix Array) 접미사 배열(Suffix Array) 접미사..
zoosso.tistory.com
구현코드
vector<int> kasai(string& txt, vector<int>& suffixArr)
{ // kasai 알고리즘
//가장 긴 접미사(원본 문자열)부터 길이가 짧아지는 순서대로 접미사를 탐색하며 최장공통접두사의 길이를 구한다.
//이 알고리즘의 핵심적인 생각은 현재 탐색하고 있는 접미사의 최장공통접두사 길이가 k라면
//다음에 탐색하는 접미사의 최장공통접두사의 길이는 k - 1 이상이라는 것이다.
//이유는 길이가 짧아지는 순으로 계산하기 때문
int n = suffixArr.size();
vector<int> lcp(n, 0);
vector<int> invSuff(n, 0);
//접미사 배열을 길이가 짧은 순으로 새로 저장한다.
for (int i = 0; i < n; i++)
invSuff[suffixArr[i]] = i;
int k = 0;
for (int i = 0; i < n; i++)
{
if (invSuff[i] == n - 1) //만약 가장 긴 부분 문자열(본 문자열)이라면 공통 접두사 존재 불가
{
k = 0;
continue;
}
//j에는 비교할 다음 문자열을 저장. 즉 접미사 배열의 다음 문자열
int j = suffixArr[invSuff[i] + 1];
// k 번째 index에서 일치 시작
// 최소 k-1개가 일치
while (i + k < n && j + k < n && txt[i + k] == txt[j + k])
k++;
lcp[invSuff[i]] = k; // lcp 배열 갱신
// 다음 탐색때는 최대 k-1까지만 가능하므로 k-- 실행
if (k > 0)
k--;
}
return lcp;
}https://kimtaehyun98.tistory.com/25
백준 9248번 - Suffix Array
백준 9248번 - Suffix Array www.acmicpc.net/problem/9248 9248번: Suffix Array Suffix Array란, 문자열 S가 있을 때 그 접미사들을 정렬해 놓은 배열이다. 예를 들어, 문자열 S=banana의 접미사는 아래와 같이..
kimtaehyun98.tistory.com
'정보 > 알고리즘' 카테고리의 다른 글
| Sqrt Decomposition(제곱근 분할법) (0) | 2022.07.28 |
|---|---|
| Meet in the middle (MITM) (0) | 2022.07.26 |
| Suffix Array(접미사 배열)멘버 마이어스Manber-Myers (0) | 2022.07.04 |
| 최소공통조상(LCA-Lowest Common Ancestor) (0) | 2022.01.22 |
| 문자열알고리즘-트라이(TRIE) (0) | 2022.01.02 |