| LCA(Lowest Common Ancestor) 란? |
LCA 란 최소 공통 조상을 찾는 알고리즘
- 두 정점 u,v 에서 가장 가까운 공통조상을 찾는 과정을 말한다.
| LCA(Lowest Common Ancestor) 구현 방법 |
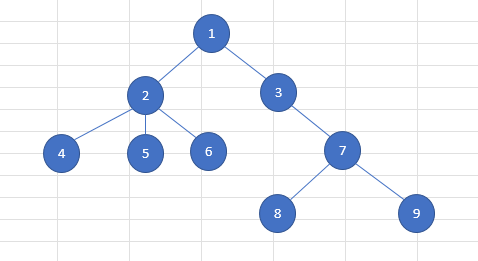
위의 그래프에서 LCA((4,8)=1 이 됩니다.
가장 단순한 방법은 한번에 하나씩 자신의 조상을 찾아 올라가는 방법입니다.
4의 조상은 2,8의 조상은 7,2의 조상은 1,7의 조상은 3,1의 조상은 루트이므로 대기,3의 조상은 1 에서 순차적으로 하나씩 찾아가다가 누군가가 먼저 지나간 자리에 도착하면 그곳이 공통조상이 됩니다.
하지만 이 알고리즘은 최대 O(N) 의 시간이 걸립니다.
https://www.acmicpc.net/problem/11438
11438번: LCA 2
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정
www.acmicpc.net
위의 문제에서는 노드 갯수가 100000개 질의 갯수가 100000 이므로 이 알고리즘으로는 최대 100억번 연산을 하게 됩니다.
그렇다면 이것보다 더 좋은 알고리즘을 찾아 봅니다.
먼저 부모에 대한 테이블을 만들어 봅니다. 알고리즘을 위해서 좀더 깊이 있는 형태로 만들어 보겠습니다.
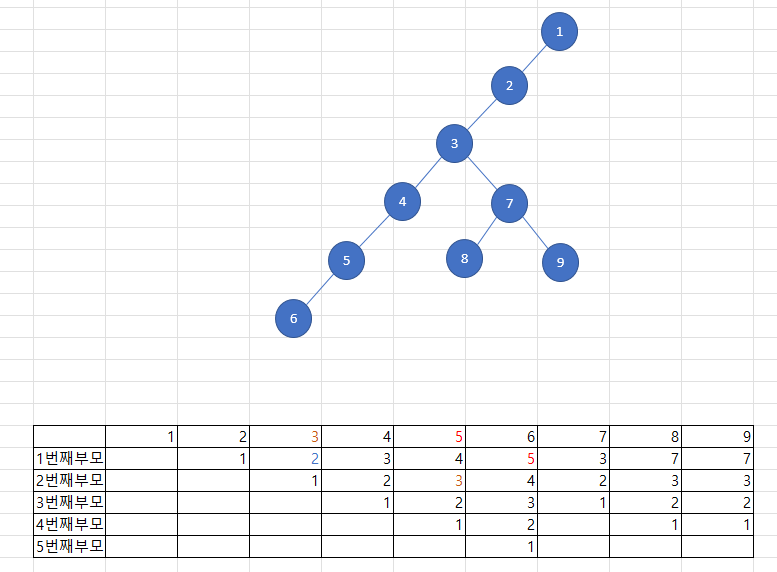
여기에서 부모를 찾아 가는 방법을 살펴 보면 6의 4번째 부모 2를 찾아 갈때 5->4->3->2 로 찾아 갈 수 있지만 이것을 2의 거듭제곱 형식으로 찾아가는 방법이 있을 수 있습니다.
먼저 2^0 위치 5를 찾아 간 후
5의 2^1 위치 3을 찾아가면 3번째 부모를 만나게 됩니다.
이때 7번째 부모를 찾고 싶은 경우 3의 위치에서 2^2 위치 값을 찾아 주면 그곳이 6의 7번째 부모의 값이 됩니다.
여기서는 4번째 부모의 위치이므로 3번째 부모위치 3의 첫번째 부모 2를 찾아 주면 됩니다.
이렇게 하면 번째 조상을 찾는 시간이 log2(N) 시간으로 단축이 됩니다.
이렇게 테이블을 만들어 보면 다음과 같이 만들 수가 있습니다.

6의 5번째 부모를 찾기 위해서는 6의 2^2(4) 위치를 찾은 후 부모 2의 위치에서 2^0 위치를 찾아 주면 됩니다.
이때 5라는 숫자는 이진수로 0101 이 되며 2^2 위치로 올라간 후 2^1 위치로 이동해 주면 됩니다.
그럼 공통조상을 찾아 봅니다.
만약 6과 7의 공통 조상을 찾는다고 하면 서로의 깊이가 많이 다릅니다.
따라서 6과 7의 깊이를 같게 만들어 주어야 합니다.
이때 깊이의 차이가 2이므로 6에서 2^1위치인 2번째 부모 위치까지 올라가면 되고 만약 그 차이가 11 차이가 난다고 이진수로 1011 이므로 2^0 위치,2^1 위치,2^3 위치 3번만에 해당 위치까지 올라 갈 수 있습니다.
이렇게 이진수를 이용하면 log2(N) 시간만에 깊이를 같게 만들 수 있습니다.
이렇게 같게 만든 위치에서 부모를 따라 가면서 공통조상을 찾을 수 있습니다.

위의 예에서 5와 9의 공통조상을 찾는 경우 오른쪽 위치부터 하나씩 비교하면 2^0 위치에서 달라지는 것을 확인 할 수 있습니다. 이때 5의 부모를 4로 놓고 9의 부모를 7로 놓고 다시 4와 7의 부모를 찾아 가면 됩니다.
| 문제풀이 |
11438번: LCA 2
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정
www.acmicpc.net
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
#define MAX_N 100010
using namespace std;
int n, m, parent[21][MAX_N], visited[MAX_N], dep[MAX_N ];
vector<int> link[MAX_N];
void dfs(int cur,int depth) {
visited[cur] = true;
dep[cur] = depth;
for (int i=0;i<link[cur].size();i++) {
if (visited[link[cur][i]]) continue;
parent[0][link[cur][i]] = cur; /// 자식의 2^0번째 부모는 자신이다.
dfs(link[cur][i], depth + 1); /// 자식을 찾아 가 보자.
}
}
void makeParent() {
int next;
for (int dept = 1; dept < 21; dept++) { ///2^20 = 1048576 이므로 2^20승 까지의 부모를 찾아 주자
for (int i = 1; i <= n; i++) {
/*
2^1 위치의 부모는 2^0(자기 부모) 의 2^0 위치의 부모(부모의 부모)에 해당한다.
2^2 위치의 부모는 2^1(자기 부모의 부모) 위치의 2^1(부모의 부모가 바라본 부모의 부모) 위치에 해당한다.
*/
next = parent[dept - 1][i];
parent[dept][i] = parent[dept - 1][next];
}
}
}
int lca(int x, int y) {
int depth;
if(dep[x]>dep[y]){
///만약 x의 깊이가 더 깊다면 x를 y의 깊이로 이동하자.
depth = dep[x] - dep[y];
for(int i=20;i>=0;i--){
if(depth & (1<<i)) {
x = parent[i][x]; /// 해당 비트 위치가 셋트 되어 있으면 그 위치로 이동하자.
}
}
} else {
///만약 x의 깊이가 더 깊다면 x를 y의 깊이로 이동하자.
depth = dep[y] - dep[x];
for(int i=20;i>=0;i--){
if(depth & (1<<i)) {
y = parent[i][y]; /// 해당 비트 위치가 셋트 되어 있으면 그 위치로 이동하자.
}
}
}
if (x == y)return x;
for (int i = 20; i >= 0; i--) {
if (parent[i][x] != parent[i][y]) { ///둘의 부모가 서로 다르면 다른 위치로 이동해 보자.
x = parent[i][x];
y = parent[i][y];
}
}
return parent[0][x];
}
int main() {
cin.tie(NULL);
cout.tie(NULL);
ios::sync_with_stdio(NULL);
//freopen("input.txt","r",stdin);
cin >> n;
int a,b;
for (int i = 0; i < n - 1; i++) {
cin >> a >> b;
link[a].push_back(b);
link[b].push_back(a);
}
dfs(1, 0); ///전처리 작업하자
makeParent();
cin >> m;
while (m--) {
cin >> a >> b;
cout << lca(a, b) << "\n";
}
return 0;
}
'정보 > 알고리즘' 카테고리의 다른 글
| LCP (Longest Common Prefix) (0) | 2022.07.07 |
|---|---|
| Suffix Array(접미사 배열)멘버 마이어스Manber-Myers (0) | 2022.07.04 |
| 문자열알고리즘-트라이(TRIE) (0) | 2022.01.02 |
| SPFA(Shortest Path Faster Algorithm) (0) | 2021.10.23 |
| [알고리즘] 2D Fenwick Tree(2차원 펜윅트리) (0) | 2021.08.27 |