생각하는 아이들

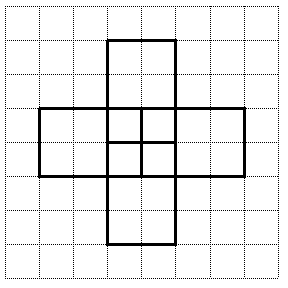
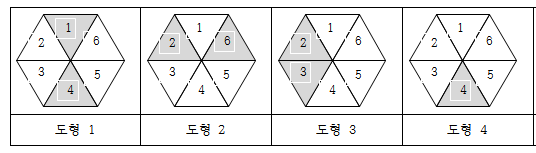
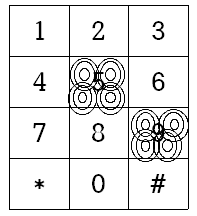
초등 4학년 - 수와 연산 : 큰수,곱셈과 나눗셈,분수의 덧셈과 뺄셈,소수의 덧셈과 뺄셈 - 규칙찾기 - 도형 : 평면도형의 이동, 삼각형, 사각형, 다각형 - 측정 : 각도 - 막대그래프,꺽은선 그래프 3학년 2학기때 배운 진분수 개념은 분자가 분모보다 작은것을 진분수라고 하는데요. 2019/11/03 - [교과수학/3-2] - 3학년 2학기 여러가지 분수 알아 보기 불러오는 중입니다... 오늘은 분모가 같은 진분수 끼리의 뺄셈에 대해서 알아 보겠습니다. 가령 3/4 - 1/4 를 그림을 그려서 확인을 해 보면 먼저 위와 같은 1을 4로 나눈것 중의 3개를 선택한 노랑색에서 1/4 를 빼면 다음과 같이 노랑색은 2개가 남습니다. 파랑색 부분이 빠진 부분 따라서 2/4만 남게 되는데요. 뺄셈에서도 덧셈과..

초등 4학년 - 수와 연산 : 큰수,곱셈과 나눗셈,분수의 덧셈과 뺄셈,소수의 덧셈과 뺄셈 - 규칙찾기 - 도형 : 평면도형의 이동, 삼각형, 사각형, 다각형 - 측정 : 각도 - 막대그래프,꺽은선 그래프 오늘은 4학년 2학기때 배우는 진분수의 덧셈에 대해 알아 보도록 하겠습니다. 3학년 2학기때 배운 진분수 개념을 다시 한번 살펴 보겠습니다. 2019/11/03 - [교과수학/3-2] - 3학년 2학기 여러가지 분수 알아 보기 불러오는 중입니다... 내용을 보면 1/5,2/5 와 같이 분자가 분모보다 작은 수를 진분수라고 합니다. 7/5 와 같이 분자가 분모보다 큰 경우를 가분수 위와 같이 자연수와 진분수로 표현한 것을 대분수라고 합니다. 이번 장에서는 진분수의 덧셈에 대해 알아 보겠습니다. 1/5 + ..

길동이는 다음과 같은 도형을 그리는 과정을 친구에게 설명하려고 한다. 도형을 한번도 보지 않은 친구가 길동이의 설명을 듣고 정확하게 그릴수 있도록 해야 한다. (단, 도형의 위치는 고려하지 않는다.) 이때 주의 할 점은 자신이 생각한 순서대로 설명한다. 또한 애매모호한 표현은 하지 않는다. 즉 원을 그린다 가 아니라 반지름이 2인 원을 그린다 와 같이 명료하게 표현을 해야 한다. 여러분이라면 어떻게 설명할지 말해 주세요. 정답예시 ...더보기 먼저 한변의 길이가 2인 정사각형을 그린다. 그리고 그 주변 4변을 기준으로 처음 그렸던 정사각형의 변에 붙여서 똑같이 길이가 2인 정사각형을 그린다. 마지막으로 처음 그린 정사각형을 4등분하여 길이가 1인 정사각형 4개를 만든다.

길동이는 어떤 규칙에 따라서 도형에 색칠을 하고 있었습니다. 이때 길순이가 들어와서 유심히 들여다 보며 다음 색깔은 여기에 칠하면 되겠네 라고 말하였습니다. 그렇다면 길순이가 가르친 색깔을 칠해야 하는 위치는 어디일까요? 정답) ...더보기 규칙을 살펴보면 다음과 같습니다. 1번에 색칠한 것은 1 -> 2 -> 3 -> 4 4번에 색칠한 것은 4 -> 6 -> 2 -> 4 길동이는 위와 같은 규칙으로 색칠하고 있었습니다. 그러면 다음에 색칠할 곳은 1번에서 출발한 곳은 1 -> 2 -> 3 -> 4 -> 5 4번에서 출발한 곳은 4 -> 6 -> 2 -> 4 -> 6 이 되겠네요. 정답은 5와 6입니다.

길동이 아버지는 비밀금고를 갖고 계시는데 오래전에 연 탓에 비밀번호를 잊어버렸습0니다. 길동이는 비밀번호를 찾기 위해 금고의 보안장치에 특수한 물질을 묻혔더니 그림과 같은 지문자국이 나타났습니다. 비밀번호가 4자리 숫자로 되어 있다면, 가능한 비밀번호를 모두 구하시오. 정답 ...더보기 5가 1개 9가 3개인 경우 5999,9599,9959,9995 (4가지) 5가 2개 9가 2개인 경우 5599,5959,5995,9559,9595,9955 (6가지) 5가 3개 9가 1개인 경우 5559,5595,5955,9555(4가지) 총 14가지 입니다. 14가지의 경우의 수를 세는 방법은 각 자리수에 2개를 선택하는 경우의 수 2 x 2 x 2 x 2 = 16 가지인데 여기서 5555, 9999 인경우를 제외하면..

길동이는 길순이에게 "너 소수가 무엇인지 알고있어?" 라고 물어 보았습니다. 길순이는 길동이에게 "그것도 몰라? 약수의 갯수가 1과 자기자신만 있는것을 소수라고 말하는 거잖아." " 2,3,5,7... 이런 수를 말하는 거잖아.." "그러면 어떤 수가 소수인지 아닌지 쉽게 판별하는 방법에 대해 알고 있어? 가령 1037이 소수인지 아닌지 빨리 알아내는 방법 같은 것 말이야" "그런 방법이 있어?" 라고 길순이 길동에게 되물었습니다. 길동이는 다음과 같이 대답했어요. " 어떤 수는 자기 자신과 1외에는 약수가 없는 것을 이용해서 1037이 어떤 소수로 나누어 지는지를 판별하면 돼..." " 가령 2,3,5,7,13... 과 같은 수로 나누어 보는 것이지" 그러자 길순이가 물었어요. " 왜 모든수에 대해서 ..

초등 3학년 - 수와 연산 : 분수와 소수,덧셈과 뺄셈,나눗셈 - 도형 : 평면도형, 원 - 길이와 시간,무게측정 - 자료의 정리 분수중에서는 10개를 5묶음으로 나눈 2개를 1/5 라고 합니다. 이렇게 10개를 기준으로 2/5 는 4개, 3/5는 6개와 같이 나타낼수 있는데요. 그렇다면 6/5 와 같은 경우는 몇개일까요? 2개짜리가 6개 있으므로 12개가 됩니다. 이렇게 1/5,2/5 와 같이 분자가 분모보다 작은 수를 진분수라고 합니다. 또한 기준이 되는 10개를 넘어서는 분수 5/5,6/5 와 같이 분자가 분모보다 크거나 같은 수를 가분수라고 합니다. 이때 5/5 는 1과 같습니다. 이 의미는 피자 한판을 5조각으로 나누었는데 이 5조각을 모두 합친 개념입니다. 이렇게 합치면 피자 한판이 되는 것처..

초등 3학년 - 수와 연산 : 분수와 소수,덧셈과 뺄셈,나눗셈 - 도형 : 평면도형, 원 - 길이와 시간,무게측정 - 자료의 정리 3학년 1학기 때에 분수라는 것을 배워 보았는데요. 2019/10/20 - [교과수학/3-1] - 3학년 1학기 똑같이 나누기 불러오는 중입니다... 한바구니에 담긴 구슬이 8개가 들어 있는데... 이것을 두 사람에게 똑같이 나누어 주려고 합니다. 이때 한사람에게 4개씩을 나누어 주게 되는데요. 이것을 전체를 1바구니를 2명으로 나눈 수 1/2 라고 표현합니다. 구슬 8 개를 2로 나눈 수 1/2은 4개가 되는데 이것은 4로 나눈수 2개 1/4 을 2개 합한 수와 동일하게 됩니다. 1/4 + 1/4 = 2/4 (4개) = 1/2(4개) 그렇다면 사탕 20개를 똑같이 5묶음으로..

초등 3학년 - 수와 연산 : 분수와 소수,덧셈과 뺄셈,나눗셈 - 도형 : 평면도형, 원 - 길이와 시간,무게측정 - 자료의 정리 원의 중심이란 컴퍼스로 원을 그릴때 중심이 되는 중심점을 의미합니다. 이때 원의 중심에서 원위의 한점과의 거리를 반지름이라고 합니다. 위와 같은 원이 있을때 A는 원의 중심, 선분 AC 또는 AB는 원의 반지름이라고 합니다. 또한 중심점을 지나는 원위의 두 점을 이은 선분 BC는 원의 지름이라고 합니다. 이때 원의 지름의 성질을 살펴 보면, 원의 지름은 한개의 원을 이등분하는 성질을 갖습니다. 또한 원의 지름은 원안에서 선분을 그을 수 있는 것중에 가장 깁니다. 원의 지름의 성질 중 하나는 원의 지름은 원의 반지름의 2배입니다. 그렇다면 위와 같은 원의 AC의 반지름이 2cm..

길동이는 순환소수가 왜 같은 수를 반복하게 될 수 밖에 없는지 그 이유가 무척 궁금했습니다. 길순이에게 혹시 그 이유가 무엇인지 물어 보았는데요. 길순이도 어떻게 설명을 해야 될지 모르다가... 멋적게 다음과 같이 설명을 이어 나갔습니다. 1/7 을 소수로 만드는 과정을 적어 볼래? 길동이는 다음과 같이 계산을 해 보았습니다. 길순이가 말했습니다. 나머지가 1 -> 3 -> 2 -> 6 -> 4 -> 5 -> 1 이 되고 다시 1이 반복 되므로 순환이 될 수 밖에 없는 거야. 여기서 7의 나머지가 0 이 되는 경우가 나타나면 순환이 끝나는 유한소수가 되는 것이지. 이때 1에서 다시 1이 되는 구간이 6마다 다시 돌아 오는 것을 순환마디라고 하거든... 그렇다면 1/13의 순환마디는 무엇일까? 정답) ....