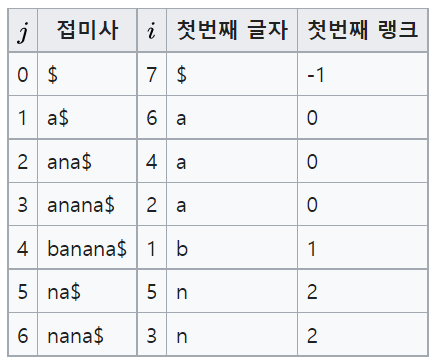
접미사 배열(https://thinkmath2020.tistory.com/3558) 자체만으로 해결 할 수 있는 문제는 거의 없다.접미사 배열과 함께 중요한 개념인 LCP(Longest Common Prefix)를 살펴 보자.LCP는 가장 긴 공통 접두사로 일반적으로 그 길이에 의미가 있다.대부분의 상황에서 Suffix Array 에 쓰이는 개념이라고 볼 수 있다. lcp[i]는 접미사 배열의 i번째 접미사와 i-1번째 접미사의 가장 긴 공통 접두사의 길이라고 정의 된다.접미사numlcpa5xana31anana13banana00na40nana22앞의 길이가 얼마만큼 크기가 같은지 찾아 주면 된다.이때 앞에서 부터 하나씩 찾는다면 길이 n 에 대해 O(n^2) 의 시간 복잡도이지만 다음과 같이 처리하면 O..